AI를 이용한 주식가격 예측에 관심이 많습니다. 인터넷에서 가져온 내용을 한국사람이 읽기 좋게 정리하여 공유합니다.
통계학적 용어와, AI분석용어가 섞여서 읽어내기 쉽지 않지만, 보다 정확한 주식예측을 위해서 다양한 접근방법을 사용하는 것을 보면서 지혜를 얻으시면 좋겠습니다.
AI의 최신 발전을 사용하여 주식 시장 움직임 예측
이 노트북에서 나는 주가 움직임을 예측하기 위한 완전한 프로세스를 만들 것입니다. 잘 따라오시면 꽤 좋은 결과를 얻을 수 있을 것입니다. 이를 위해 Recurrent Neural Network의 일종인 LSTM 을 Generator로 하고 Convolutional Neural Network인 CNN 을 Discriminator로 사용하는 GAN( Generative Adversarial Network )을 사용합니다. 우리는 시계열 데이터를 예측하려는 명백한 이유로 LSTM을 사용합니다. GAN, 특히 CNN을 판별자로 사용합니다.
가장 어려운 부분은 GAN입니다. GAN을 성공적으로 교육하는 데 매우 까다로운 부분은 올바른 하이퍼파라미터 세트를 얻는 것입니다. 이러한 이유로 우리는 GAN의 하이퍼파라미터(탐색 대 착취 딜레마)를 변경하는 시기와 방법을 결정하기 위해 베이지안 최적화 (가우시안 프로세스와 함께) 및 강화 학습 (RL)을 사용할 것입니다. 강화 학습을 만들 때 Rainbow 및 PPO 와 같은 현장에서 가장 최근의 발전을 사용할 것입니다 .
다양한 유형의 입력 데이터를 사용할 것입니다. 주식의 과거 거래 데이터 및 기술 지표와 함께 NLP 의 최신 기술 ('Bidirectional Embedding Representations from Transformers', BERT , 일종의 NLP 전이 학습 사용)을 사용하여 감정 분석(기본 분석의 소스로 사용)을 생성합니다. ), 전체 추세 방향 추출을 위한 푸리에 변환 , 다른 상위 수준 기능을 식별하기 위한 누적 자동 인코더 , 상관 자산 찾기를 위한 고유 포트폴리오 , 자동 회귀 통합 이동 평균( ARIMA) 주식에 대한 가능한 한 많은 정보, 패턴, 종속성 등을 캡처하기 위해 주식 함수 근사화 등을 위해. 우리 모두 알다시피 (데이터)가 많을수록 더 즐겁습니다. 주가 움직임을 예측하는 것은 매우 복잡한 작업이므로 다양한 관점에서 주식에 대해 더 많이 알수록 변화가 더 커집니다.
모든 신경망을 생성하기 위해 MXNet과 그 고급 API인 Gluon을 사용하고 여러 GPU에서 훈련합니다.
참고: 거의 모든 알고리즘과 기술의 배후에 있는 수학 및 메커니즘에 대해 자세히 알아보려고 노력했지만 이 노트북은 머신/딥 러닝 또는 주식 시장이 작동하는 방식을 명시적으로 설명하기 위한 것이 아닙니다. 목적은 오히려 주가 움직임을 정확하게 예측하기 위해 다양한 기술과 알고리즘을 사용할 수 있는 방법을 보여주고 각 단계에서 각 기술을 사용하는 이유와 유용성에 대한 근거를 제공하는 것입니다.
그림 1 - 작업의 전체 아키텍처

1. 소개
특정 주식이 특정 방향으로 움직이기 위해서는 수백만 개의 이벤트와 전제 조건이 있기 때문에 주식 시장을 정확하게 예측하는 것은 복잡한 작업입니다. 따라서 이러한 전제 조건을 최대한 많이 포착할 수 있어야 합니다. 우리는 또한 몇 가지 중요한 가정을 해야 합니다. 1) 시장은 100% 무작위가 아니며, 2) 역사는 반복되고, 3) 시장은 사람들의 합리적인 행동을 따르고, 4) 시장은 ' 완벽 '합니다.
Goldman Sachs (NYSE: GS) 의 가격 변동을 예측해 보겠습니다 . 이를 위해 2010년 1월 1일부터 2018년 12월 31일까지 일일 종가를 사용합니다(교육 목적으로 7년, 검증 목적으로 2년). 우리는 'Goldman Sachs'와 'GS'라는 용어를 같은 의미로 사용할 것 입니다.
3. 데이터
GS(골드만삭스)의 주가가 오르느냐 내리느냐에 어떤 영향을 미치는지 이해해야 합니다. 그것은 사람들이 전체적으로 생각하는 것입니다. 따라서 가능한 한 많은 정보(다양한 측면과 각도에서 주식을 묘사)를 통합해야 합니다. (일별 데이터 - 1,585일을 사용하여 다양한 알고리즘을 훈련하고(보유한 데이터의 70%) 다음 680일(테스트 데이터)을 예측합니다. 그런 다음 예측된 결과를 테스트(홀드아웃) 데이터와 비교합니다. . 데이터의 각 유형( 기능 이라고 함)은 이후 섹션에서 자세히 설명하지만 상위 수준 개요로 사용할 기능은 다음과 같습니다.
- 상관 자산 - 이들은 다른 자산입니다(상품, FX, 지수 또는 고정 소득 증권과 같은 반드시 주식이 아닌 모든 유형). Goldman Sachs와 같은 대기업은 분명히 고립된 세계에서 '살지' 않습니다. 경쟁업체, 고객, 세계 경제, 지정학적 상황, 재정적 상황 등 많은 외부 요인에 의존하고 상호 작용합니다. 통화 정책, 자본에 대한 접근 등 세부 사항은 나중에 나열됩니다.
- 기술 지표 - 많은 투자자들이 기술 지표를 따릅니다. 가장 인기 있는 지표를 독립적인 기능으로 포함합니다. 7일 및 21일 이동 평균, 지수 이동 평균, 모멘텀, 볼린저 밴드, MACD.
- 펀더멘털 분석 - 주가가 상승 또는 하락할지 여부를 나타내는 매우 중요한 기능입니다. 펀더멘털 분석에 사용할 수 있는 기능은
1) 10-K, 10-Q 리포트를 이용한 회사 실적 분석, ROE, P/E 등 분석(사용하지 않음),
2) 뉴스 등 두 가지 기능이 있습니다.-
잠재적인 뉴스는 특정 방향으로 주식을 잠재적으로 움직일 수 있는 다가오는 이벤트를 나타낼 수 있습니다. Goldman Sachs에 대한 모든 일일 뉴스를 읽고 그날의 Goldman Sachs에 대한 전체 감정이 긍정적인지, 중립적인지 또는 부정적인지(0에서 1까지의 점수로) 추출합니다. 많은 투자자들이 뉴스를 면밀히 읽고 (물론 부분적으로) 뉴스를 기반으로 투자 결정을 내리기 때문에 오늘 Goldman Sachs에 대한 뉴스가 매우 긍정적이라면 내일 주식이 급등할 가능성이 다소 높습니다. 한 가지 중요한 점은 나중에 절대적으로 모든 기능(이 기능 포함)에 대해 기능 중요도(GS의 움직임을 나타내는 정도)를 수행하고 사용할지 여부를 결정할 것입니다.
정확한 감정 예측을 생성하기 위해 신경 언어 처리( NLP )를 사용합니다. 감정 분류 스톡 뉴스 감정 추출을 위한 전이 학습을 위해 Google에서 최근에 발표한 NLP 접근 방식인 BERT 를 사용 합니다.
- 푸리에 변환 - 일일 종가와 함께 여러 장기 및 단기 추세를 일반화하기 위해 푸리에 변환을 생성합니다. 이러한 변환을 사용하여 많은 노이즈(랜덤 워크)를 제거하고 실제 주식 이동의 근사치를 생성합니다. 추세 근사치가 있으면 LSTM 네트워크가 예측 추세를 더 정확하게 선택하는 데 도움이 될 수 있습니다.
- ARIMA( Autoregressive Integrated Moving Average ) - 이것은 시계열 데이터의 미래 값을 예측하는 데 가장 널리 사용되는 기술 중 하나였습니다(신경망 이전 시대). 그것을 추가하고 그것이 중요한 예측 기능으로 나오는지 봅시다.
- Stacked autoencoders - 앞서 언급한 대부분의 기능(기본 분석, 기술 분석 등)은 수십 년의 연구 끝에 사람들이 발견했습니다. 그러나 아마도 우리는 뭔가를 놓쳤을 것입니다. 막대한 양의 데이터 포인트, 이벤트, 자산, 차트 등으로 인해 사람들이 이해할 수 없는 숨겨진 상관관계가 있을 수 있습니다. 누적된 자동 인코더(신경망 유형)를 사용하면 컴퓨터의 성능을 사용할 수 있으며 아마도 새로운 유형의 기능을 찾을 수 있습니다. 주식 움직임에 영향을 미칩니다. 인간의 언어로는 이러한 기능을 이해할 수 없지만 GAN에서는 사용할 것입니다.
- 옵션 가격에서 이상 감지를 위한 Deep Unsupervised Learning . 한 가지 기능을 더 사용할 것입니다. 매일 Goldman Sachs 주식에 대한 90일 콜 옵션 가격을 추가합니다. 옵션 가격 자체는 많은 데이터를 결합합니다. 옵션 계약의 가격은 주식의 미래 가치에 따라 달라집니다(애널리스트는 콜 옵션의 가장 정확한 가격을 제시하기 위해 가격을 예측하기도 합니다). 심층 비지도 학습( 자체 구성 지도 )을 사용하여 매일의 가격에서 이상 현상을 찾아내려고 노력할 것입니다. 이상 현상(예: 가격의 급격한 변화)은 LSTM이 전체 주식 패턴을 학습하는 데 유용할 수 있는 이벤트를 나타낼 수 있습니다.
다음으로 기능이 너무 많기 때문에 몇 가지 중요한 단계를 수행해야 합니다.
- 데이터의 '품질'에 대한 통계 검사를 수행합니다. 만든 데이터에 결함이 있으면 알고리즘이 아무리 정교하더라도 결과는 긍정적이지 않습니다. 검사에는 데이터가 이분산성, 다중 공선성 또는 직렬 상관 관계로 인해 영향을 받지 않는지 확인하는 작업이 포함됩니다.
- 기능 중요도를 만듭니다. 기능(예: 다른 주식 또는 기술 지표)이 우리가 예측하려는 주식에 대한 설명력이 없는 경우 신경망 훈련에 사용할 필요가 없습니다. 부스트 트리 회귀 알고리즘의 일종인 XGBoost (eXtreme Gradient Boosting)를 사용 합니다.
데이터 준비의 마지막 단계로 자동 인코더에서 생성된 기능의 차원을 줄이기 위해 주성분 분석( PCA )을 사용하여 고유 포트폴리오 를 생성합니다.
from utils import *
import time
import numpy as np
from mxnet import nd, autograd, gluon
from mxnet.gluon import nn, rnn
import mxnet as mx
import datetime
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.decomposition import PCA
import math
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
import xgboost as xgb
from sklearn.metrics import accuracy_scoreimport warnings
warnings.filterwarnings("ignore")context = mx.cpu(); model_ctx=mx.cpu()
mx.random.seed(1719)참고 : 이 섹션(3. 데이터)의 목적은 데이터 전처리를 보여주고 다양한 데이터 소스를 사용하는 근거를 제시하는 것이므로 전체 데이터의 하위 집합(훈련에 사용됨)만 사용하겠습니다.
def parser(x):
return datetime.datetime.strptime(x,'%Y-%m-%d')dataset_ex_df = pd.read_csv('data/panel_data_close.csv', header=0, parse_dates=[0], date_parser=parser)dataset_ex_df[['Date', 'GS']].head(3).dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| 2009-12-31 | 168.839996 |
| 2010-01-04 | 173.080002 |
| 2010-01-05 | 176.139999 |
print('There are {} number of days in the dataset.'.format(dataset_ex_df.shape[0]))There are 2265 number of days in the dataset.
지난 9년간의 주식을 시각화해 봅시다. 파선 세로선은 훈련 데이터와 테스트 데이터 사이의 구분을 나타냅니다.
plt.figure(figsize=(14, 5), dpi=100)
plt.plot(dataset_ex_df['Date'], dataset_ex_df['GS'], label='Goldman Sachs stock')
plt.vlines(datetime.date(2016,4, 20), 0, 270, linestyles='--', colors='gray', label='Train/Test data cut-off')
plt.xlabel('Date')
plt.ylabel('USD')
plt.title('Figure 2: Goldman Sachs stock price')
plt.legend()
plt.show()
num_training_days = int(dataset_ex_df.shape[0]*.7)
print('Number of training days: {}. Number of test days: {}.'.format(num_training_days, \
dataset_ex_df.shape[0]-num_training_days))Number of training days: 1585. Number of test days: 680.
3.1. 상관 자산
앞에서 설명한 것처럼 GS뿐만 아니라 다른 자산을 기능으로 사용할 것입니다.
그렇다면 다른 어떤 자산이 GS의 주식 움직임에 영향을 미칠까요? 회사, 비즈니스 라인, 경쟁 구도, 종속 관계, 공급업체 및 클라이언트 유형 등에 대한 올바른 이해는 올바른 관련 자산 집합을 선택하는 데 매우 중요합니다.
- 첫 번째는 GS(골드만삭스)와 유사한 회사 입니다. JPMorgan Chase와 Morgan Stanley 등을 데이터 세트에 추가합니다.
- 투자 은행으로서 골드만삭스는 세계 경제 에 의존합니다 . 나쁘거나 불안정한 경제는 M&A 또는 IPO가 없으며 독점 거래 수익이 제한될 수 있음을 의미합니다. 이것이 바로 우리가 글로벌 경제 지표를 포함하는 이유입니다. 또한 LIBOR (USD 및 GBP 표시) 비율을 포함할 것입니다. 분석가가 이러한 비율을 설정하기 위해 경제 충격을 고려할 수 있기 때문입니다 .
- 일일 변동성 지수( VIX ) - 이전 항목에서 설명한 이유 때문입니다.
- 복합 지수 - NASDAQ 및 NYSE(미국), FTSE100(영국), Nikkei225(일본), Hang Seng 및 BSE Sensex(APAC) 지수.
- 통화 - 글로벌 무역은 통화 이동 방식에 여러 번 반영되므로 통화 바스켓(예: USDJPY, GBPUSD 등)을 기능으로 사용합니다.
전반적으로 데이터 세트에는 모든 자산의 일일 가격인 72개의 다른 자산이 있습니다.
3.2. 기술적 지표
우리는 기술 지표가 무엇이고 왜 사용하는지 이미 다루었으므로 바로 코드로 넘어가겠습니다. GS만을 위한 기술적 지표를 만들어 드립니다.
def get_technical_indicators(dataset):
# Create 7 and 21 days Moving Average
dataset['ma7'] = dataset['price'].rolling(window=7).mean()
dataset['ma21'] = dataset['price'].rolling(window=21).mean()
# Create MACD
dataset['26ema'] = pd.ewma(dataset['price'], span=26)
dataset['12ema'] = pd.ewma(dataset['price'], span=12)
dataset['MACD'] = (dataset['12ema']-dataset['26ema'])
# Create Bollinger Bands
dataset['20sd'] = pd.stats.moments.rolling_std(dataset['price'],20)
dataset['upper_band'] = dataset['ma21'] + (dataset['20sd']*2)
dataset['lower_band'] = dataset['ma21'] - (dataset['20sd']*2)
# Create Exponential moving average
dataset['ema'] = dataset['price'].ewm(com=0.5).mean()
# Create Momentum
dataset['momentum'] = dataset['price']-1
return datasetdataset_TI_df = get_technical_indicators(dataset_ex_df[['GS']])dataset_TI_df.head().dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| 2010-02-01 | 153.130005 | 152.374285 | 164.220476 | 160.321839 | 156.655072 | -3.666767 | 9.607375 | 183.435226 | 145.005726 | 152.113609 | 152.130005 | 5.024735 |
| 2010-02-02 | 156.940002 | 152.777143 | 163.653809 | 160.014868 | 156.700048 | -3.314821 | 9.480630 | 182.615070 | 144.692549 | 155.331205 | 155.940002 | 5.049471 |
| 2010-02-03 | 157.229996 | 153.098572 | 162.899047 | 159.766235 | 156.783365 | -2.982871 | 9.053702 | 181.006450 | 144.791644 | 156.597065 | 156.229996 | 5.051329 |
| 2010-02-04 | 150.679993 | 153.069999 | 161.686666 | 158.967168 | 155.827031 | -3.140137 | 8.940246 | 179.567157 | 143.806174 | 152.652350 | 149.679993 | 5.008500 |
| 2010-02-05 | 154.160004 | 153.449999 | 160.729523 | 158.550196 | 155.566566 | -2.983631 | 8.151912 | 177.033348 | 144.425699 | 153.657453 | 153.160004 | 5.031483 |
그래서 우리는 모든 거래일에 대한 기술적 지표(MACD, 볼린저 밴드 등 포함)를 가지고 있습니다. 총 12개의 기술 지표가 있습니다.
이러한 지표의 지난 400일을 시각화해 보겠습니다.
def plot_technical_indicators(dataset, last_days):
plt.figure(figsize=(16, 10), dpi=100)
shape_0 = dataset.shape[0]
xmacd_ = shape_0-last_days
dataset = dataset.iloc[-last_days:, :]
x_ = range(3, dataset.shape[0])
x_ =list(dataset.index)
# Plot first subplot
plt.subplot(2, 1, 1)
plt.plot(dataset['ma7'],label='MA 7', color='g',linestyle='--')
plt.plot(dataset['price'],label='Closing Price', color='b')
plt.plot(dataset['ma21'],label='MA 21', color='r',linestyle='--')
plt.plot(dataset['upper_band'],label='Upper Band', color='c')
plt.plot(dataset['lower_band'],label='Lower Band', color='c')
plt.fill_between(x_, dataset['lower_band'], dataset['upper_band'], alpha=0.35)
plt.title('Technical indicators for Goldman Sachs - last {} days.'.format(last_days))
plt.ylabel('USD')
plt.legend()
# Plot second subplot
plt.subplot(2, 1, 2)
plt.title('MACD')
plt.plot(dataset['MACD'],label='MACD', linestyle='-.')
plt.hlines(15, xmacd_, shape_0, colors='g', linestyles='--')
plt.hlines(-15, xmacd_, shape_0, colors='g', linestyles='--')
plt.plot(dataset['log_momentum'],label='Momentum', color='b',linestyle='-')
plt.legend()
plt.show()plot_technical_indicators(dataset_TI_df, 400)
3.3. 기초분석
근본적인 분석을 위해 GS에 대한 모든 일일 뉴스에 대한 감정 분석을 수행합니다. 마지막에 시그모이드를 사용하면 결과는 0과 1 사이가 됩니다. 점수가 0에 가까울수록 뉴스가 더 부정적입니다(1에 가까울수록 긍정적인 감정을 나타냄). 매일 평균 일일 점수(0과 1 사이의 숫자)를 생성하고 기능으로 추가합니다.
3.3.1. 트랜스포머의 양방향 임베딩 표현 - BERT
뉴스를 긍정 또는 부정(또는 중립)으로 분류하기 위해 사전 훈련된 언어 표현인 BERT 를 사용합니다.
사전 훈련된 BERT 모델은 이미 MXNet/Gluon에서 사용할 수 있습니다. 인스턴스화하고 두 개의 (임의의 숫자) Dense레이어를 추가하고 softmax로 이동하기만 하면 됩니다. 점수는 0에서 1까지입니다.
# just import bert
import bertBERT 및 NLP 부분의 세부 사항으로 들어가는 것은 이 노트북의 범위에 있지 않습니다.
언어 처리와 관련하여 확실히 유망한 BERT 전용 새 저장소를 만들 것입니다..
3.4. 추세 분석을 위한 푸리에 변환
푸리에 변환 은 함수를 사용하여 일련의 사인파(진폭 및 프레임이 다름)를 생성합니다. 결합되면 이러한 사인파는 원래 함수에 근접합니다. 수학적으로 말하면 변환은 다음과 같습니다.
G(에프)=∫-∞∞g(티)이자형-나2파이에프티디티
푸리에 변환을 사용하여 골드만삭스 주식의 글로벌 및 로컬 추세를 추출하고 노이즈를 약간 제거합니다. 어떻게 작동하는지 봅시다.
data_FT = dataset_ex_df[['Date', 'GS']]close_fft = np.fft.fft(np.asarray(data_FT['GS'].tolist()))
fft_df = pd.DataFrame({'fft':close_fft})
fft_df['absolute'] = fft_df['fft'].apply(lambda x: np.abs(x))
fft_df['angle'] = fft_df['fft'].apply(lambda x: np.angle(x))plt.figure(figsize=(14, 7), dpi=100)
fft_list = np.asarray(fft_df['fft'].tolist())
for num_ in [3, 6, 9, 100]:
fft_list_m10= np.copy(fft_list); fft_list_m10[num_:-num_]=0
plt.plot(np.fft.ifft(fft_list_m10), label='Fourier transform with {} components'.format(num_))
plt.plot(data_FT['GS'], label='Real')
plt.xlabel('Days')
plt.ylabel('USD')
plt.title('Figure 3: Goldman Sachs (close) stock prices & Fourier transforms')
plt.legend()
plt.show()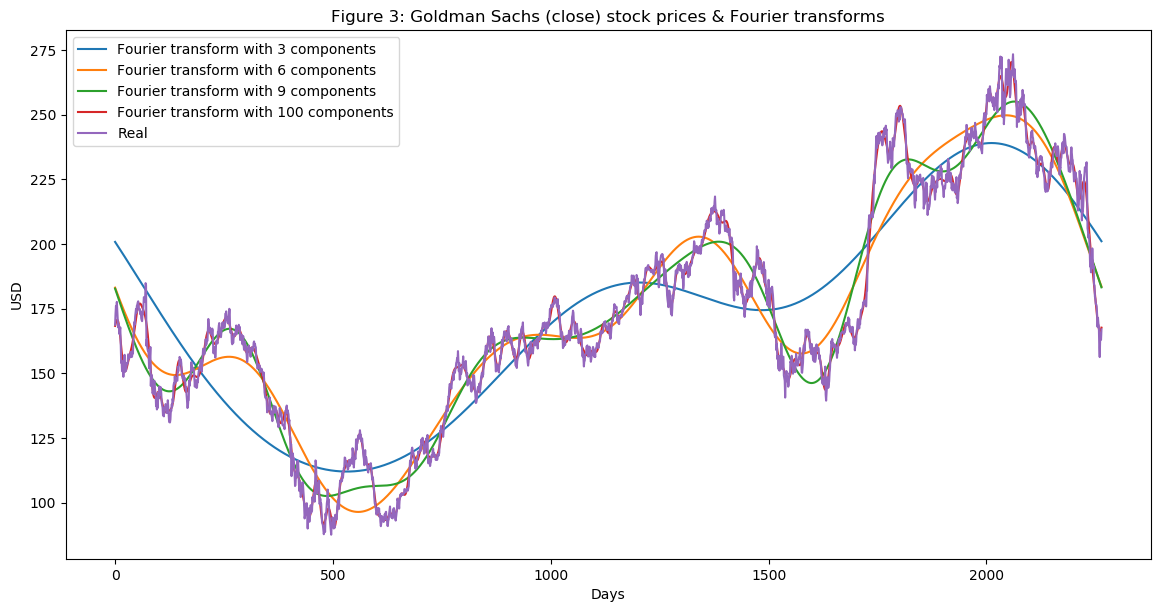
그림 3에서 볼 수 있듯이 우리가 사용하는 푸리에 변환의 구성 요소가 많을수록 근사 함수가 실제 주가에 더 가까워집니다(100개 구성 요소 변환은 원래 함수와 거의 동일합니다. 빨간색과 보라색 선이 거의 겹칩니다). 우리는 장단기 추세를 추출하기 위해 푸리에 변환을 사용하므로 3, 6 및 9 구성 요소로 변환을 사용합니다. 3개의 구성 요소가 있는 변환이 장기 추세 역할을 한다고 추론할 수 있습니다.
데이터를 노이즈 제거하는 데 사용되는 또 다른 기술은 웨이블릿 호출 입니다. 웨이블릿과 푸리에 변환은 유사한 결과를 나타내므로 푸리에 변환만 사용합니다.
from collections import deque
items = deque(np.asarray(fft_df['absolute'].tolist()))
items.rotate(int(np.floor(len(fft_df)/2)))
plt.figure(figsize=(10, 7), dpi=80)
plt.stem(items)
plt.title('Figure 4: Components of Fourier transforms')
plt.show()
3.5. 기능으로서의 ARIMA
ARIMA 는 시계열 데이터를 예측하는 기술입니다., ARIMA가 최종 예측으로 사용되지는 않을 것이지만, 주식을 약간 제거하고 (아마도) 몇 가지 새로운 패턴이나 특징을 추출하는 기술로 사용할 것입니다.
from statsmodels.tsa.arima_model import ARIMA
from pandas import DataFrame
from pandas import datetime
series = data_FT['GS']
model = ARIMA(series, order=(5, 1, 0))
model_fit = model.fit(disp=0)
print(model_fit.summary()) ARIMA Model Results
==============================================================================
Dep. Variable: D.GS No. Observations: 2264
Model: ARIMA(5, 1, 0) Log Likelihood -5465.888
Method: css-mle S.D. of innovations 2.706
Date: Wed, 09 Jan 2019 AIC 10945.777
Time: 10:28:07 BIC 10985.851
Sample: 1 HQIC 10960.399
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0011 0.054 -0.020 0.984 -0.106 0.104
ar.L1.D.GS -0.0205 0.021 -0.974 0.330 -0.062 0.021
ar.L2.D.GS 0.0140 0.021 0.665 0.506 -0.027 0.055
ar.L3.D.GS -0.0030 0.021 -0.141 0.888 -0.044 0.038
ar.L4.D.GS 0.0026 0.021 0.122 0.903 -0.039 0.044
ar.L5.D.GS -0.0522 0.021 -2.479 0.013 -0.093 -0.011
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.7595 -0.0000j 1.7595 -0.5000
AR.2 -0.5700 -1.7248j 1.8165 -0.3008
AR.3 -0.5700 +1.7248j 1.8165 0.3008
AR.4 1.4743 -1.0616j 1.8168 -0.0993
AR.5 1.4743 +1.0616j 1.8168 0.0993
-----------------------------------------------------------------------------
from pandas.tools.plotting import autocorrelation_plot
autocorrelation_plot(series)
plt.figure(figsize=(10, 7), dpi=80)
plt.show() 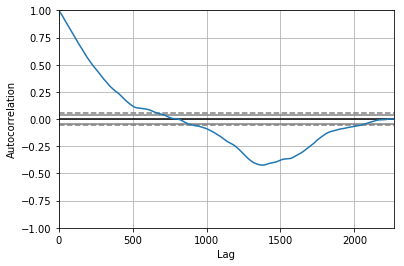
<Figure size 800x560 with 0 Axes>
from pandas import read_csv
from pandas import datetime
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error
X = series.values
size = int(len(X) * 0.66)
train, test = X[0:size], X[size:len(X)]
history = [x for x in train]
predictions = list()
for t in range(len(test)):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test[t]
history.append(obs)error = mean_squared_error(test, predictions)
print('Test MSE: %.3f' % error)Test MSE: 10.151
# Plot the predicted (from ARIMA) and real prices
plt.figure(figsize=(12, 6), dpi=100)
plt.plot(test, label='Real')
plt.plot(predictions, color='red', label='Predicted')
plt.xlabel('Days')
plt.ylabel('USD')
plt.title('Figure 5: ARIMA model on GS stock')
plt.legend()
plt.show()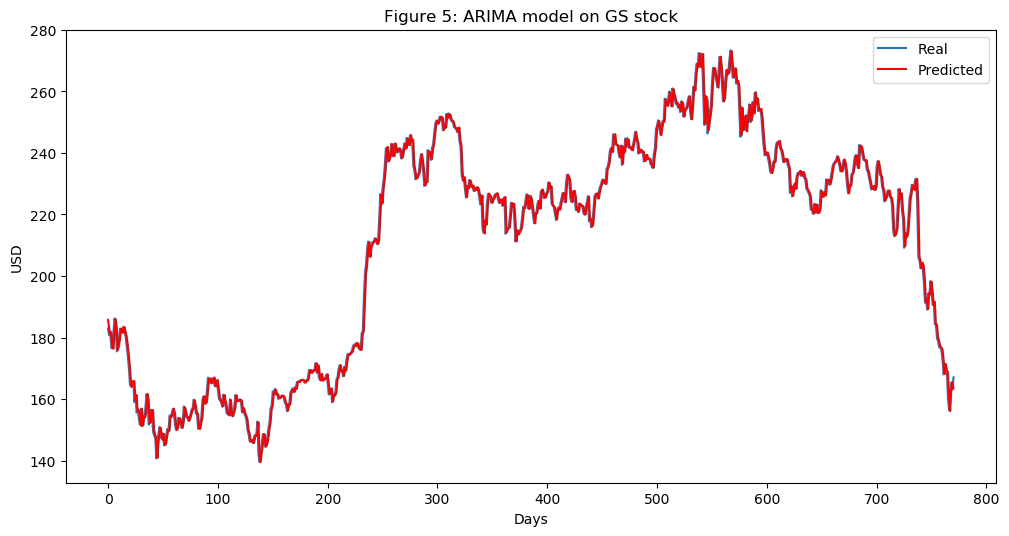
그림 5에서 볼 수 있듯이 ARIMA는 실제 주가에 대한 아주 좋은 근사치를 제공합니다. 앞에서 언급한 바와 같이 가능한 한 Goldman Sachs에 대한 많은 기능과 패턴을 캡처하기를 원하기 때문에 ARIMA를 통해 예측된 가격을 LSTM의 입력 기능으로 사용할 것입니다. 우리는 10.151의 MSE(평균 제곱 오차)를 테스트합니다. 그 자체로는 나쁜 결과가 아니지만(테스트 데이터가 많다는 점을 고려하면) 여전히 LSTM의 기능으로만 사용할 것입니다.
3.6. 통계 확인
데이터의 품질이 좋은지 확인하는 것은 외부 모델에 매우 중요합니다. 데이터가 적합한지 확인하기 위해 기본 데이터 분포에 근본적인 오류가 있다는 사실로 인해 손상되지 않고 달성하고 관찰한 결과가 실제로 실제인지 확인하기 위해 몇 가지 간단한 검사를 수행합니다.
3.6.1. 이분산성, 다중공선성, 계열상관
- 조건부 이분산성 은 오차 항(회귀에 의한 예측 값과 실제 값의 차이)이 데이터에 종속될 때 발생합니다. 예를 들어 오차 항은 데이터 포인트(x축을 따라)가 커질 때 커집니다.
- 다중 공선 성은 오류 항(잔차라고도 함)이 서로 의존하는 경우입니다.
- 직렬 상관관계 는 하나의 데이터(특징)가 다른 특징의 공식(또는 완전히 반대)인 경우입니다.
코드가 간단하고 심층 학습 부분에 더 중점을 두지만 데이터는 정성적이므로 여기서는 코드를 다루지 않을 것 입니다.
3.7. 기능 엔지니어링
print('Total dataset has {} samples, and {} features.'.format(dataset_total_df.shape[0], \
dataset_total_df.shape[1]))Total dataset has 2265 samples, and 112 features.
따라서 모든 유형의 데이터(상관 자산, 기술 지표, 기본 분석, 푸리에 및 아리마)를 추가한 후 2,265일 동안 총 112개의 기능이 있습니다(앞서 언급했듯이 1,585일만 훈련 데이터용임). .
또한 오토인코더에서 생성된 몇 가지 기능이 추가될 것입니다.
3.7.1. XGBoost의 기능 중요도
너무 많은 기능을 가지고 있기 때문에 우리는 그것들 모두가 GS 주식이 취할 방향을 실제로 나타내는지 여부를 고려해야 합니다. 예를 들어, 우리는 LIBOR의 변화가 경제의 변화를 나타낼 수 있고, 이는 다시 GS 주식 행동의 변화를 나타낼 수 있다고 생각하기 때문에 데이터 세트에 USD 표시 LIBOR 비율을 포함했습니다. 하지만 우리는 테스트가 필요합니다. 기능 중요도를 테스트하는 방법에는 여러 가지가 있지만 우리가 적용할 방법은 분류 및 회귀 문제 모두에서 최상의 결과를 제공하는 XGBoost를 사용하는 것입니다.
기능 데이터 세트가 상당히 크기 때문에 여기에서는 프레젠테이션을 위해 기술 지표만 사용합니다. 실제 기능 중요도 테스트 중에 선택된 모든 기능이 다소 중요한 것으로 판명되었으므로 GAN을 교육할 때 어떤 것도 제외하지 않을 것입니다.
def get_feature_importance_data(data_income):
data = data_income.copy()
y = data['price']
X = data.iloc[:, 1:]
train_samples = int(X.shape[0] * 0.65)
X_train = X.iloc[:train_samples]
X_test = X.iloc[train_samples:]
y_train = y.iloc[:train_samples]
y_test = y.iloc[train_samples:]
return (X_train, y_train), (X_test, y_test)# Get training and test data
(X_train_FI, y_train_FI), (X_test_FI, y_test_FI) = get_feature_importance_data(dataset_TI_df)regressor = xgb.XGBRegressor(gamma=0.0,n_estimators=150,base_score=0.7,colsample_bytree=1,learning_rate=0.05)xgbModel = regressor.fit(X_train_FI,y_train_FI, \
eval_set = [(X_train_FI, y_train_FI), (X_test_FI, y_test_FI)], \
verbose=False)eval_result = regressor.evals_result()training_rounds = range(len(eval_result['validation_0']['rmse']))교육을 관찰하고 과적합이 있는지 확인하기 위해 교육 및 검증 오류를 플로팅해 보겠습니다(과적합이 없음).
plt.scatter(x=training_rounds,y=eval_result['validation_0']['rmse'],label='Training Error')
plt.scatter(x=training_rounds,y=eval_result['validation_1']['rmse'],label='Validation Error')
plt.xlabel('Iterations')
plt.ylabel('RMSE')
plt.title('Training Vs Validation Error')
plt.legend()
plt.show()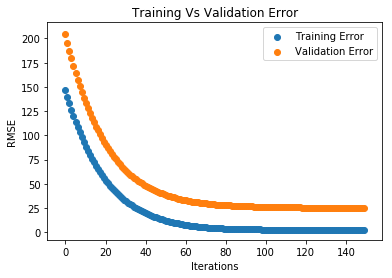
fig = plt.figure(figsize=(8,8))
plt.xticks(rotation='vertical')
plt.bar([i for i in range(len(xgbModel.feature_importances_))], xgbModel.feature_importances_.tolist(), tick_label=X_test_FI.columns)
plt.title('Figure 6: Feature importance of the technical indicators.')
plt.show()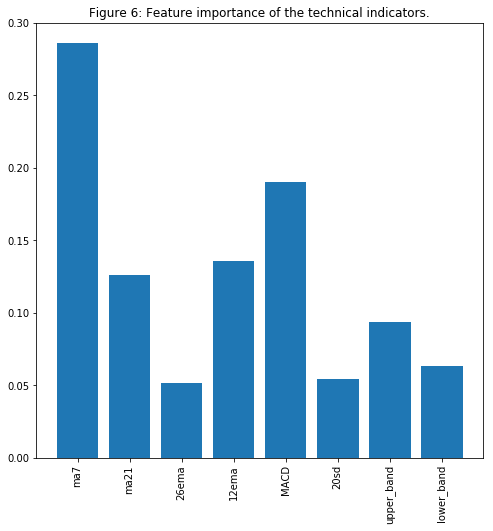
MA7, MACD 및 BB가 중요한 기능 중 하나라는 것은 놀라운 일이 아닙니다(주식 거래 경험이 있는 사람들에게는).
전체 데이터 세트에 대해 기능 중요도를 수행하기 위해 동일한 논리를 따랐습니다. 소수의 기능과 비교할 때 교육 시간이 더 오래 걸리고 결과를 읽기가 조금 더 어려웠습니다.
3.8. Stacked Autoencoder로 상위 수준 기능 추출
오토인코더로 진행하기 전에 대체 활성화 기능을 살펴보겠습니다.
3.8.1. 활성화 기능 - GELU(Gaussian Error)
GELU -Gaussian Error Linear Unites가 최근 제안 되었습니다 . 이 논문에서 저자는 GELU를 사용하는 신경망이 활성화로 ReLU를 사용하는 신경망을 능가하는 몇 가지 사례를 보여줍니다. 뉴스 정서 분석에 사용한 NLP 접근 방식인 BERTgelu 에서도 사용됩니다 .
오토인코더에는 GELU를 사용합니다.
참고 : 아래 셀은 GELU 수학의 논리를 보여줍니다. 활성화 함수로 실제 구현된 것은 아닙니다. MXNet 내부에 GELU를 구현해야 했습니다. 코드를 따르고 변경 act_type='relu'하면 act_type='gelu'MXNet 구현을 변경하지 않는 한 작동하지 않습니다. GELU의 MXNet 구현에 액세스하려면 전체 프로젝트에서 풀 요청을 만드십시오.
def gelu(x):
return 0.5 * x * (1 + math.tanh(math.sqrt(2 / math.pi) * (x + 0.044715 * math.pow(x, 3))))
def relu(x):
return max(x, 0)
def lrelu(x):
return max(0.01*x, x)GELU, ReLU및를 시각화해 보겠습니다 LeakyReLU(마지막 것은 주로 GAN에서 사용되며 우리도 사용함).
plt.figure(figsize=(15, 5))
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=.5, hspace=None)
ranges_ = (-10, 3, .25)
plt.subplot(1, 2, 1)
plt.plot([i for i in np.arange(*ranges_)], [relu(i) for i in np.arange(*ranges_)], label='ReLU', marker='.')
plt.plot([i for i in np.arange(*ranges_)], [gelu(i) for i in np.arange(*ranges_)], label='GELU')
plt.hlines(0, -10, 3, colors='gray', linestyles='--', label='0')
plt.title('Figure 7: GELU as an activation function for autoencoders')
plt.ylabel('f(x) for GELU and ReLU')
plt.xlabel('x')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot([i for i in np.arange(*ranges_)], [lrelu(i) for i in np.arange(*ranges_)], label='Leaky ReLU')
plt.hlines(0, -10, 3, colors='gray', linestyles='--', label='0')
plt.ylabel('f(x) for Leaky ReLU')
plt.xlabel('x')
plt.title('Figure 8: LeakyReLU')
plt.legend()
plt.show()
참고 : 이 노트북의 향후 버전에서는 U-Net ( 링크 )을 사용하여 실험하고 컨볼루션 계층을 활용하고 주식의 기본 이동 패턴에 대해 더 많은 기능을 추출(및 생성)하려고 합니다. Dense지금은 레이어 로만 만든 간단한 오토인코더를 사용하겠습니다 .
참고 : 이후 버전에서 살펴볼 한 가지는 디코더의 마지막 레이어를 제거하는 것입니다. 일반적으로 자동 인코더에서 인코더 수 == 디코더 수입니다. 그러나 우리는 디코더의 마지막 레이어를 건너뛸 수 있도록 (동일한 입력을 생성하는 대신) 더 높은 수준의 기능을 추출하기를 원합니다. 교육 중에 동일한 수의 레이어로 인코더와 디코더를 생성하여 이를 달성하지만, 출력을 생성할 때 더 높은 수준의 기능을 포함할 것이므로 유일한 레이어 옆에 있는 레이어를 사용합니다.
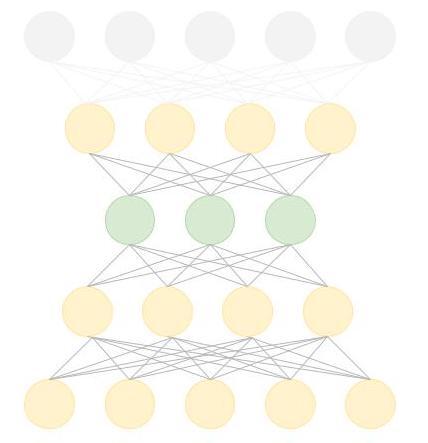
batch_size = 64
n_batches = VAE_data.shape[0]/batch_size
VAE_data = VAE_data.values
train_iter = mx.io.NDArrayIter(data={'data': VAE_data[:num_training_days,:-1]}, \
label={'label': VAE_data[:num_training_days, -1]}, batch_size = batch_size)
test_iter = mx.io.NDArrayIter(data={'data': VAE_data[num_training_days:,:-1]}, \
label={'label': VAE_data[num_training_days:,-1]}, batch_size = batch_size)model_ctx = mx.cpu()
class VAE(gluon.HybridBlock):
def __init__(self, n_hidden=400, n_latent=2, n_layers=1, n_output=784, \
batch_size=100, act_type='relu', **kwargs):
self.soft_zero = 1e-10
self.n_latent = n_latent
self.batch_size = batch_size
self.output = None
self.mu = None
super(VAE, self).__init__(**kwargs)
with self.name_scope():
self.encoder = nn.HybridSequential(prefix='encoder')
for i in range(n_layers):
self.encoder.add(nn.Dense(n_hidden, activation=act_type))
self.encoder.add(nn.Dense(n_latent*2, activation=None))
self.decoder = nn.HybridSequential(prefix='decoder')
for i in range(n_layers):
self.decoder.add(nn.Dense(n_hidden, activation=act_type))
self.decoder.add(nn.Dense(n_output, activation='sigmoid'))
def hybrid_forward(self, F, x):
h = self.encoder(x)
#print(h)
mu_lv = F.split(h, axis=1, num_outputs=2)
mu = mu_lv[0]
lv = mu_lv[1]
self.mu = mu
eps = F.random_normal(loc=0, scale=1, shape=(self.batch_size, self.n_latent), ctx=model_ctx)
z = mu + F.exp(0.5*lv)*eps
y = self.decoder(z)
self.output = y
KL = 0.5*F.sum(1+lv-mu*mu-F.exp(lv),axis=1)
logloss = F.sum(x*F.log(y+self.soft_zero)+ (1-x)*F.log(1-y+self.soft_zero), axis=1)
loss = -logloss-KL
return lossn_hidden=400 # neurons in each layer
n_latent=2
n_layers=3 # num of dense layers in encoder and decoder respectively
n_output=VAE_data.shape[1]-1
net = VAE(n_hidden=n_hidden, n_latent=n_latent, n_layers=n_layers, n_output=n_output, batch_size=batch_size, act_type='gelu')net.collect_params().initialize(mx.init.Xavier(), ctx=mx.cpu())
net.hybridize()
trainer = gluon.Trainer(net.collect_params(), 'adam', {'learning_rate': .01})print(net)VAE(
(encoder): HybridSequential(
(0): Dense(None -> 400, Activation(relu))
(1): Dense(None -> 400, Activation(relu))
(2): Dense(None -> 400, Activation(relu))
(3): Dense(None -> 4, linear)
)
(decoder): HybridSequential(
(0): Dense(None -> 400, Activation(relu))
(1): Dense(None -> 400, Activation(relu))
(2): Dense(None -> 400, Activation(relu))
(3): Dense(None -> 11, Activation(sigmoid))
)
)
따라서 인코더와 디코더 모두에 3개의 레이어(각각 400개의 뉴런 포함)가 있습니다.
n_epoch = 150
print_period = n_epoch // 10
start = time.time()
training_loss = []
validation_loss = []
for epoch in range(n_epoch):
epoch_loss = 0
epoch_val_loss = 0
train_iter.reset()
test_iter.reset()
n_batch_train = 0
for batch in train_iter:
n_batch_train +=1
data = batch.data[0].as_in_context(mx.cpu())
with autograd.record():
loss = net(data)
loss.backward()
trainer.step(data.shape[0])
epoch_loss += nd.mean(loss).asscalar()
n_batch_val = 0
for batch in test_iter:
n_batch_val +=1
data = batch.data[0].as_in_context(mx.cpu())
loss = net(data)
epoch_val_loss += nd.mean(loss).asscalar()
epoch_loss /= n_batch_train
epoch_val_loss /= n_batch_val
training_loss.append(epoch_loss)
validation_loss.append(epoch_val_loss)
"""if epoch % max(print_period, 1) == 0:
print('Epoch {}, Training loss {:.2f}, Validation loss {:.2f}'.\
format(epoch, epoch_loss, epoch_val_loss))"""
end = time.time()
print('Training completed in {} seconds.'.format(int(end-start)))Training completed in 62 seconds.
dataset_total_df['Date'] = dataset_ex_df['Date']vae_added_df = mx.nd.array(dataset_total_df.iloc[:, :-1].values)print('The shape of the newly created (from the autoencoder) features is {}.'.format(vae_added_df.shape))The shape of the newly created (from the autoencoder) features is (2265, 112).
오토인코더에서 112개의 추가 기능을 만들었습니다. 높은 수준의 기능(전체 패턴)만 갖고 싶기 때문에 PCA(Principal Component Analysis:주성분분석)를 사용하여 새로 생성된 112개 기능에 고유 포트폴리오를 만듭니다. 이렇게 하면 데이터의 차원(열 수)이 줄어듭니다. Eigen 포트폴리오의 설명 기능은 원래 112개 기능과 동일합니다.
참고 다시 한 번 말하지만 이는 순전히 실험적입니다. 설명된 논리가 성립할지 100% 확신할 수 없습니다. AI 및 딥 러닝의 다른 모든 것과 마찬가지로 이것은 예술이며 실험이 필요합니다.
3.8.2. PCA(주성분분석)를 사용한 고유 포트폴리오
# We want the PCA to create the new components to explain 80% of the variance
pca = PCA(n_components=.8)x_pca = StandardScaler().fit_transform(vae_added_df)principalComponents = pca.fit_transform(x_pca)principalComponents.n_components_84
따라서 분산의 80%를 설명하려면 84개(112개 중) 기능만이 필요합니다. 그러나 이것은 여전히 많은 것입니다. 따라서 지금은 오토인코더 생성 기능을 포함하지 않습니다. Dense나는 중간 레이어(마지막 레이어가 아님)에서 출력을 가져와 이를 30개의 뉴런이 있는 다른 레이어에 연결하는 오토인코더 아키텍처를 만드는 작업을 할 것 입니다. 따라서 1) 더 높은 수준의 기능만 추출하고 2) 열 수가 훨씬 적습니다.
4. 생성적 적대 신경망(GAN)
그림 9: 간단한 GAN 아키텍처

GAN은 어떻게 작동합니까?
독자가 주가 움직임을 예측하는 데 GAN을 사용하는 이유를 완전히 이해할 수 있도록 GAN의 작동 방식에 대한 균형을 잡고 높은 수준의 개요를 제공하려고 노력할 것입니다. GAN에 익숙하다면 이 섹션과 다음 섹션을 건너뛰어도 됩니다
GAN 네트워크는 Generator ($G$)와 Discriminator ($D$)의 두 가지 모델로 구성됩니다. GAN 훈련 단계는 다음과 같습니다.
- 생성기는 임의의 데이터를 사용합니다(노이즈는지), 실제 데이터와 구별할 수 없거나 매우 근접한 데이터를 '생성'하려고 합니다. 목적은 실제 데이터의 분포를 학습하는 것입니다.
- 무작위로 실제 또는 생성된 데이터는 분류자 역할을 하는 Discriminator에 적합하며 데이터가 Generator에서 오는지 또는 실제 데이터인지 이해하려고 시도합니다.디들어오는 샘플의 실제 데이터 세트에 대한 (분포) 확률을 추정합니다. ( 아래 섹션 4.2 에서 두 분포를 비교해보세요 ).
- 그런 다음,G그리고디결합되어 생성기를 통해 다시 전파됩니다. 따라서 제너레이터의 손실은 제너레이터와 판별자 모두에 따라 달라집니다. 이는 Generator가 실제 데이터 분포에 대해 학습하는 데 도움이 되는 단계입니다. 생성기가 실제 데이터(동일한 분포를 가짐)를 생성하는 데 제대로 작동하지 않는 경우 Discriminator의 작업은 실제 데이터 세트에서 생성된 것을 매우 쉽게 구별할 수 있습니다. 따라서 Discriminator의 손실은 매우 적습니다. 판별기 손실이 작으면 발전기 손실이 더 커 집니다( $L(D, G)$에 대한 아래 방정식 참조 ). 이것은 Discriminator를 생성하는 것을 약간 까다롭게 만듭니다. Discriminator가 너무 좋으면 항상 Generator가 크게 손실되어 Generator가 학습할 수 없기 때문입니다.
- Discriminator가 더 이상 생성된 실제 데이터를 구별할 수 없을 때까지 프로세스가 계속됩니다.
함께 결합하면,디그리고G일종의 minmax 게임을 하는 것과 같습니다(생성기가 판별기를 속이 려고 시도하여 가짜 예제에 대한 확률을 높입니다. 즉, $\mathbb{E} {z \sim p {z}(z)} [\log ( 1 - D(G(z)))]$. Discriminator는 Generator에서 오는 데이터를 분리하려고 합니다.디(G(지)), $\mathbb{E} {x \sim p {r}(x)} [\log D(x)]$)를 최대화합니다. 그러나 분리된 손실 함수가 있으면 둘 다 어떻게 함께 수렴할 수 있는지 명확하지 않습니다(그래서 우리는 Wasserstein GAN과 같은 일반 GAN에 대한 일부 개선 사항을 사용합니다). 전체적으로 결합된 손실 함수는 다음과 같습니다.
엘(디,G)=이자형엑스~피아르 자형(엑스)[통나무디(엑스)]+이자형지~피지(지)[통나무(1-디(G(지)))]
4.1. 주식 시장 예측에 GAN을 사용하는 이유는 무엇입니까?
GAN( Generative Adversarial Networks )은 최근 사실적인 이미지, 그림 및 비디오 클립을 만드는 데 주로 사용되었습니다. 우리의 경우와 같이 시계열 데이터를 예측하는 데 사용되는 GAN의 응용 프로그램은 많지 않습니다. 그러나 주요 아이디어는 동일해야 합니다. 우리는 미래 주식 움직임을 예측하려고 합니다. 미래에 GS 주식의 패턴과 행동은 거의 동일해야 합니다(완전히 다른 방식으로 운영되기 시작하거나 경제가 급격하게 변화하지 않는 한). 따라서 우리는 이미 가지고 있는 것과 유사한(물론 절대적으로 동일하지는 않음) 분포를 가질 미래를 위한 데이터를 '생성'하고자 합니다. 즉, 과거 거래 데이터입니다. 따라서 이론상으로는 작동해야 합니다.
우리의 경우 LSTM 을 시계열 생성기로 사용하고 CNN 을 판별자로 사용합니다.
4.2. Metropolis-Hastings GAN 및 Wasserstein GAN
참고: 다음 두 섹션에서는 GAN에 대한 경험이 있다고 가정합니다.
I. 메트로폴리스-헤이스팅스 GAN
기존 GAN에 대한 최근 개선 사항이 Uber의 엔지니어링 팀에서 나왔고 이를 MHGAN( Metropolis-Hastings GAN )이라고 합니다. Uber의 접근 방식 뒤에 있는 아이디어는 Google과 University of California, Berkeley에서 만든 DRS ( Discriminator Rejection Sampling )라는 또 다른 접근 방식과 다소 유사합니다. 기본적으로 GAN을 훈련할 때 Generator($G$)를 더 잘 훈련시키기 위한 목적으로만 Discriminator($D$)를 사용합니다. 종종 GAN을 학습한 후에는디더 이상. 그러나 MHGAN과 DRS는디생성된 샘플을 선택하기 위해G실제 데이터 분포에 가깝습니다(MHGAN이 샘플링에 Markov Chain Monte Carlo(MCMC)를 사용한다는 점에서 약간의 차이가 있음)
MHGAN 은 _G(독립적인 노이즈 입력에서 생성됨G-지0에게지케이아래 그림에서). 그런 다음 K 개의 출력($x'_0$에서엑스케이′′) 수락 규칙(식별자에서 생성됨)에 따라 현재 샘플을 수락할지 또는 마지막으로 수락된 샘플을 유지할지 여부를 결정합니다. 마지막으로 보관된 출력은 다음의 실제 출력으로 간주되는 출력입니다.G.
참고 : MHGAN은 원래 pytorch에서 Uber에 의해 구현되었습니다. MXNet/Gluon으로만 옮겼습니다.
그림 10: MHGAN의 시각적 표현(원본 Uber 게시물 에서 ).

II. Wasserstein GAN
GAN 교육은 매우 어렵습니다. 모델이 수렴되지 않을 수 있으며 모드 붕괴가 쉽게 발생할 수 있습니다. 우리는 Wasserstein GAN- WGAN 이라는 수정된 GAN을 사용할 것입니다 .
다시 말하지만, 자세한 내용은 다루지 않겠지만 가장 주목할 만한 사항은 다음과 같습니다.
- 우리가 알고 있듯이 GAN의 주요 목표는 생성기가 무작위 노이즈를 우리가 모방하려는 일부 주어진 데이터로 변환하기 시작하는 것입니다. 따라서 두 분포 간의 유사성을 비교하는 아이디어는 GAN에서 매우 중요합니다. 가장 널리 사용되는 두 가지 메트릭은 다음과 같습니다.
- KL 발산 (Kullback–Leibler) -디케이엘(피|큐)=∫엑스피(엑스)통나무피(엑스)큐(엑스)디엑스.디케이엘때 제로피(엑스)와 동등하다큐(엑스),
- JS 다이버전스 (Jensen-Shannon) -디제이에스(피|큐)=12디케이엘(피|피+큐2)+12디케이엘(큐|피+큐2). JS 발산은 0과 1로 제한되며 KL 발산과 달리 대칭적이고 더 부드럽습니다. 손실이 KL에서 JS 발산으로 전환되었을 때 GAN 교육에서 상당한 성공을 거두었습니다.
- WGAN은 Wasserstein 거리 $W(p_r, p_g) = \frac{1}{K} \sup_{| 에프 | L \leq K} \mathbb{E} {x \sim p_r}[f(x)] - \mathbb{E}_{x \sim p_g}[f(x)]$ (여기서에스유피손실 함수(Earth Mover 's distance라고도 함)로, 일반적으로 하나의 모래 더미를 다른 더미로 이동하는 것으로 해석되며 두 더미는 서로 다른 확률 분포를 가지며 변환 중에 최소 에너지를 사용함) . KL 및 JS 다이버전스와 비교하여 Wasserstein 메트릭은 부드러운 측정값을 제공합니다(다이버전스의 급격한 점프 없이). 이것은 경사 하강 중에 안정적인 학습 프로세스를 생성하는 데 훨씬 더 적합합니다.
- 또한 KL 및 JS와 비교할 때 Wasserstein 거리는 거의 모든 곳에서 미분 가능합니다. 아시다시피, 역전파 동안 우리는 기울기를 생성하기 위해 손실 함수를 미분하고 가중치를 업데이트합니다. 따라서 미분 가능한 손실 함수를 갖는 것이 매우 중요합니다.
4.4. 생성기 - 1계층 RNN
4.4.1. LSTM 또는 GRU
앞서 언급했듯이 생성기는 RNN(Recurrent Neural Network) 유형인 LSTM 네트워크입니다. RNN은 모든 이전 데이터 포인트를 추적하고 시간이 지남에 따라 발전하는 패턴을 캡처할 수 있기 때문에 시계열 데이터에 사용됩니다. 그 특성상 RNN은 기울기 소실 로 인해 많은 시간을 겪습니다 . 즉, 훈련 중에 가중치가 받는 변화가 너무 작아서 변경되지 않아 네트워크가 최소 손실로 수렴할 수 없게 됩니다. 그래디언트가 너무 커지는 경우를 관찰할 수 있습니다. 이를 그래디언트 폭발 이라고 하지만 이에 대한 해결책은 매우 간단합니다. 즉, 그래디언트가 일정한 수를 초과하기 시작하면 그래디언트를 잘라내는 것입니다(예: 그래디언트 클리핑). 이 문제를 해결하는 두 가지 수정 사항인 Gated Recurrent Unit(GRU ) 및 장단기 기억( LSTM ).
둘 사이의 가장 큰 차이점은 다음과 같습니다.
1) GRU에는 2개의 게이트(업데이트 및 재설정)가 있고 LSTM에는 4개의 게이트(업데이트, 입력, 무시 및 출력)가 있습니다.
2) LSTM은 내부 메모리 상태를 유지하지만 GRU는 그렇지 않습니다.
3) LSTM은 출력 게이트 전에 비선형성(시그모이드)을 적용하지만 GRU는 적용하지 않습니다.
대부분의 경우 LSTM과 GRU는 정확도 측면에서 유사한 결과를 제공하지만 GRU는 훈련 가능한 매개변수가 훨씬 적기 때문에 계산 집약도가 훨씬 낮습니다. 그러나 LSTM은 훨씬 더 많이 사용됩니다.
엄밀히 말하면 LSTM 셀(게이트)의 수학은 다음과 같습니다.
g티=탄(엑스티여엑스g+시간티-1여시간g+비g),
나티=σ(엑스티여엑스나+시간티-1여시간나+비나),
에프티=σ(엑스티여엑스에프+시간티-1여시간에프+비에프),
영형티=σ(엑스티여엑스영형+시간티-1여시간영형+비영형),
씨티=에프티⊙씨티-1+나티⊙g티,
시간티=영형티⊙탄(씨티),
어디⊙요소별 곱셈 연산자이며 모든엑스=[엑스1,엑스2,…,엑스케이]⊤∈아르 자형케이두 가지 활성화 기능:,
σ(엑스)=[11+경험치(-엑스1),…,11+경험치(-엑스케이)]]⊤,
탄(엑스)=[1-경험치(-2엑스1)1+경험치(-2엑스1),…,1-경험치(-2엑스케이)1+경험치(-2엑스케이)]⊤
4.4.2. LSTM 아키텍처
LSTM 아키텍처는 매우 간단합니다. 하나의 LSTM레이어에는 112개의 입력 유닛(데이터 세트에 112개의 기능이 있으므로)과 500개의 숨겨진 유닛이 있고, 하나 Dense의 레이어에는 1개의 출력이 있습니다. 매일 가격입니다. 이니셜라이저는 Xavier이며 L1 손실을 사용합니다.
gan_num_features = dataset_total_df.shape[1]
sequence_length = 17
class RNNModel(gluon.Block):
def __init__(self, num_embed, num_hidden, num_layers, bidirectional=False, \
sequence_length=sequence_length, **kwargs):
super(RNNModel, self).__init__(**kwargs)
self.num_hidden = num_hidden
with self.name_scope():
self.rnn = rnn.LSTM(num_hidden, num_layers, input_size=num_embed, \
bidirectional=bidirectional, layout='TNC')
self.decoder = nn.Dense(1, in_units=num_hidden)
def forward(self, inputs, hidden):
output, hidden = self.rnn(inputs, hidden)
decoded = self.decoder(output.reshape((-1, self.num_hidden)))
return decoded, hidden
def begin_state(self, *args, **kwargs):
return self.rnn.begin_state(*args, **kwargs)
lstm_model = RNNModel(num_embed=gan_num_features, num_hidden=500, num_layers=1)
lstm_model.collect_params().initialize(mx.init.Xavier(), ctx=mx.cpu())
trainer = gluon.Trainer(lstm_model.collect_params(), 'adam', {'learning_rate': .01})
loss = gluon.loss.L1Loss()LSTM 레이어에서 500개의 뉴런을 사용하고 Xavier 초기화를 사용합니다. 정규화를 위해 L1을 사용합니다. LSTMMXNet에서 인쇄한 대로 내부에 무엇이 있는지 봅시다 .
print(lstm_model)RNNModel(
(rnn): LSTM(112 -> 500, TNC)
(decoder): Dense(500 -> 1, linear)
)
보시다시피 LSTM의 입력은 112개의 기능( dataset_total_df.shape[1])이며 LSTM 레이어의 500개 뉴런으로 이동한 다음 단일 출력인 주가 값으로 변환됩니다.
LSTM의 논리는 다음과 같습니다. 우리는 17( sequence_length)일의 데이터(다시 말하지만 데이터는 매일 GS 주식의 주가 + 그날의 다른 모든 기능(상관된 자산, 정서 등)임) 예측을 시도합니다. 18일.
다른 게시물에서는 다음과 같이 바닐라 LSTM을 수정하는 것이 더 유익한지 살펴보겠습니다.
- 양방향 LSTM 레이어 사용 - 이론적으로 데이터 세트의 끝에서 처음으로 뒤로 이동하면 LSTM이 주식 이동 패턴을 파악하는 데 도움이 될 수 있습니다.
- 적층형 RNN 아키텍처 사용 - 하나의 LSTM 레이어뿐만 아니라 2개 이상 포함. 그러나 이는 데이터가 많지 않기 때문에(1,585일 분량의 데이터만 있음) 결국 모델을 과대적합할 수 있으므로 위험할 수 있습니다.
- GRU 탐색 - 이미 설명했듯이 GRU의 셀은 훨씬 더 간단합니다.
- RNN에 어텐션 벡터를 추가 합니다.
4.4.3. 학습률 스케줄러
가장 중요한 하이퍼파라미터 중 하나는 학습률입니다. 거의 모든 옵티마이저(예: SGD, Adam 또는 RMSProp)의 학습 속도를 설정하는 것은 수렴 속도와 네트워크의 궁극적인 성능을 모두 제어하기 때문에 신경망을 훈련할 때 매우 중요합니다. 가장 간단한 학습 속도 전략 중 하나는 훈련 프로세스 전체에서 고정된 학습 속도를 유지하는 것입니다. 작은 학습률을 선택하면 옵티마이저가 좋은 솔루션을 찾을 수 있지만 초기 수렴 속도가 제한됩니다. 시간 경과에 따라 학습률을 변경하면 이러한 상충 관계를 극복할 수 있습니다.
이와 같은 최근 논문 은 수렴 및 시간 측면에서 훈련 중 전역 학습률을 변경하는 이점을 보여줍니다.
class TriangularSchedule():
def __init__(self, min_lr, max_lr, cycle_length, inc_fraction=0.5):
self.min_lr = min_lr
self.max_lr = max_lr
self.cycle_length = cycle_length
self.inc_fraction = inc_fraction
def __call__(self, iteration):
if iteration <= self.cycle_length*self.inc_fraction:
unit_cycle = iteration * 1 / (self.cycle_length * self.inc_fraction)
elif iteration <= self.cycle_length:
unit_cycle = (self.cycle_length - iteration) * 1 / (self.cycle_length * (1 - self.inc_fraction))
else:
unit_cycle = 0
adjusted_cycle = (unit_cycle * (self.max_lr - self.min_lr)) + self.min_lr
return adjusted_cycle
class CyclicalSchedule():
def __init__(self, schedule_class, cycle_length, cycle_length_decay=1, cycle_magnitude_decay=1, **kwargs):
self.schedule_class = schedule_class
self.length = cycle_length
self.length_decay = cycle_length_decay
self.magnitude_decay = cycle_magnitude_decay
self.kwargs = kwargs
def __call__(self, iteration):
cycle_idx = 0
cycle_length = self.length
idx = self.length
while idx <= iteration:
cycle_length = math.ceil(cycle_length * self.length_decay)
cycle_idx += 1
idx += cycle_length
cycle_offset = iteration - idx + cycle_length
schedule = self.schedule_class(cycle_length=cycle_length, **self.kwargs)
return schedule(cycle_offset) * self.magnitude_decay**cycle_idxschedule = CyclicalSchedule(TriangularSchedule, min_lr=0.5, max_lr=2, cycle_length=500)
iterations=1500
plt.plot([i+1 for i in range(iterations)],[schedule(i) for i in range(iterations)])
plt.title('Learning rate for each epoch')
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.show()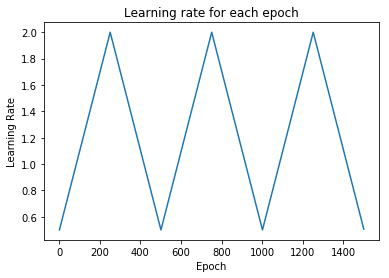
4.4.4. 과적합 및 편향-분산 절충을 방지하는 방법
기능과 신경망이 많으면 과적합을 방지하고 전체 손실을 염두에 두어야 합니다.
과적합을 방지하기 위해 몇 가지 기술을 사용합니다(LSTM뿐만 아니라 CNN 및 자동 인코더에서도).
- 데이터 품질 보장 . 우리는 이미 통계 검사를 수행했으며 데이터가 다중 공선성 또는 직렬 자기 상관으로 인해 어려움을 겪지 않는지 확인했습니다. 또한 각 기능에 대해 기능 중요도 검사를 수행했습니다. 마지막으로 초기 기능 선택(예: 상관 자산 선택, 기술 지표 등)은 주식 시장 작동 방식 이면의 메커니즘에 대한 일부 도메인 지식으로 수행되었습니다.
- 정규화 (또는 가중치 페널티). 가장 널리 사용되는 두 가지 정규화 기술은 LASSO( L1 ) 및 Ridge( L2 )입니다.). L1은 평균 절대 오차를 더하고 L2는 손실에 평균 제곱 오차를 더합니다. 기본적인 차이점은 다음과 같습니다. LASSO 회귀(L1)는 변수 선택과 매개변수 축소를 모두 수행하는 반면 Ridge 회귀는 매개변수 축소만 수행하고 모델의 모든 계수를 포함하게 됩니다. 상관 변수가 있는 경우 능선 회귀가 선호되는 선택일 수 있습니다. 또한 능선 회귀는 최소 제곱 추정값의 분산이 더 큰 상황에서 가장 잘 작동합니다. 따라서 모델 목표에 따라 다릅니다. 두 가지 정규화 유형의 영향은 상당히 다릅니다. 둘 다 큰 가중치에 페널티를 주지만 L1 정규화는 0에서 미분할 수 없는 함수로 이어집니다. L2 정규화는 더 작은 가중치를 선호하지만 L1 정규화는 0이 되는 가중치를 선호합니다. 그래서, L1 정규화를 사용하면 매개변수가 더 적은 희소 모델로 끝날 수 있습니다. 두 경우 모두 L1 및 L2 정규화 모델의 매개변수가 "수축"되지만 L1 정규화의 경우 축소는 모델의 복잡성(매개변수 수)에 직접적인 영향을 미칩니다. 정확하게 능선 회귀는 최소 제곱 추정값의 분산이 더 큰 상황에서 가장 잘 작동합니다. L1은 이상값에 더 강하고, 데이터가 희박할 때 사용되며 기능 중요도를 생성합니다. 우리는 L1을 사용할 것입니다. 능선 회귀는 최소 제곱 추정값의 분산이 더 큰 상황에서 가장 잘 작동합니다. L1은 이상값에 더 강하고, 데이터가 희박할 때 사용되며 기능 중요도를 생성합니다. 우리는 L1을 사용할 것입니다. 능선 회귀는 최소 제곱 추정값의 분산이 더 큰 상황에서 가장 잘 작동합니다. L1은 이상값에 더 강하고, 데이터가 희박할 때 사용되며 기능 중요도를 생성합니다. 우리는 L1을 사용할 것입니다.
- 드롭아웃 . 드롭아웃 레이어는 숨겨진 레이어의 노드를 무작위로 제거합니다..
복잡한 신경망을 구축할 때 또 다른 중요한 고려 사항은 편향-분산 절충입니다. 기본적으로 네트워크를 학습할 때 발생하는 오류는 바이어스, 분산 및 기약 오류 - σ(노이즈 및 무작위성으로 인한 오류)의 함수입니다. 절충의 가장 간단한 공식은 다음과 같습니다.
이자형아르 자형아르 자형영형아르 자형=비나ㅏ에스2+Vㅏ아르 자형나ㅏN씨이자형+σ
- 바이어스 . 바이어스는 훈련된(훈련 데이터 세트에서) 알고리즘이 보이지 않는 데이터를 얼마나 잘 일반화할 수 있는지 측정합니다. 높은 편향(과소적합)은 모델이 보이지 않는 데이터에서 제대로 작동할 수 없음을 의미합니다.
- 분산 . 분산은 데이터 세트의 변화에 대한 모델의 민감도를 측정합니다. 높은 분산은 과적합입니다.
4.5. 판별기 - 일차원 CNN
4.5.1. 왜 CNN을 판별자로 사용합니까?
우리는 일반적으로 이미지와 관련된 작업(분류, 컨텍스트 추출 등)에 CNN을 사용합니다. 그들은 특징에서 특징을 추출하는 데 매우 강력합니다. 예를 들어 개 이미지에서 첫 번째 컨볼루션 레이어는 가장자리를 감지하고 두 번째는 원을 감지하기 시작하며 세 번째는 코를 감지합니다. 우리의 경우 데이터 포인트는 작은 추세를 형성하고, 작은 추세는 더 크게 형성되며, 추세는 패턴을 형성합니다. CNN의 기능 감지 기능은 GS 주가 움직임의 패턴에 대한 정보를 추출하는 데 사용할 수 있습니다.
CNN을 사용하는 또 다른 이유는 CNN이 공간 데이터에서 잘 작동하기 때문입니다. 즉, 데이터 포인트가 흩어져 있는 것보다 서로 더 가까운 데이터 포인트가 서로 더 관련이 있다는 의미입니다. 이는 시계열 데이터에 적용됩니다. 우리의 경우 각 데이터 포인트(각 기능에 대한)는 연속된 날에 대한 것입니다. 두 날이 서로 가까울수록 서로 더 관련이 있다고 가정하는 것은 당연합니다. 한 가지 고려해야 할 사항(이 작업에서 다루지 않음)은 계절성과 이것이 CNN의 작업을 어떻게 변경할 수 있는지입니다.
참고 : 이 노트북의 다른 많은 부분과 마찬가지로 시계열 데이터에 CNN을 사용하는 것은 실험적입니다. 수학적 또는 기타 증명을 제공하지 않고 결과를 검사합니다. 그리고 결과는 다른 데이터, 활성화 기능 등을 사용하여 달라질 수 있습니다.
4.5.1. CNN 아키텍처
그림 11: CNN 아키텍처의 상위 수준 개요.

GAN 내부의 CNN 코드는 다음과 같습니다.
num_fc = 512
# ... other parts of the GAN
cnn_net = gluon.nn.Sequential()
with net.name_scope():
# Add the 1D Convolutional layers
cnn_net.add(gluon.nn.Conv1D(32, kernel_size=5, strides=2))
cnn_net.add(nn.LeakyReLU(0.01))
cnn_net.add(gluon.nn.Conv1D(64, kernel_size=5, strides=2))
cnn_net.add(nn.LeakyReLU(0.01))
cnn_net.add(nn.BatchNorm())
cnn_net.add(gluon.nn.Conv1D(128, kernel_size=5, strides=2))
cnn_net.add(nn.LeakyReLU(0.01))
cnn_net.add(nn.BatchNorm())
# Add the two Fully Connected layers
cnn_net.add(nn.Dense(220, use_bias=False), nn.BatchNorm(), nn.LeakyReLU(0.01))
cnn_net.add(nn.Dense(220, use_bias=False), nn.Activation(activation='relu'))
cnn_net.add(nn.Dense(1))
# ... other parts of the GANCNN을 인쇄해 봅시다.
print(cnn_net)Sequential(
(0): Conv1D(None -> 32, kernel_size=(5,), stride=(2,))
(1): LeakyReLU(0.01)
(2): Conv1D(None -> 64, kernel_size=(5,), stride=(2,))
(3): LeakyReLU(0.01)
(4): BatchNorm(axis=1, eps=1e-05, momentum=0.9, fix_gamma=False, use_global_stats=False, in_channels=None)
(5): Conv1D(None -> 128, kernel_size=(5,), stride=(2,))
(6): LeakyReLU(0.01)
(7): BatchNorm(axis=1, eps=1e-05, momentum=0.9, fix_gamma=False, use_global_stats=False, in_channels=None)
(8): Dense(None -> 220, linear)
(9): BatchNorm(axis=1, eps=1e-05, momentum=0.9, fix_gamma=False, use_global_stats=False, in_channels=None)
(10): LeakyReLU(0.01)
(11): Dense(None -> 220, linear)
(12): Activation(relu)
(13): Dense(None -> 1, linear)
)
4.6. 초매개변수
우리가 추적하고 최적화할 하이퍼파라미터는 다음과 같습니다.
- batch_size: LSTM과 CNN의 배치 크기
- cnn_lr: CNN의 학습률
- strides: CNN의 보폭 수
- lrelu_alpha: GAN의 LeakyReLU에 대한 알파
- batchnorm_momentum: CNN에서 배치 정규화를 위한 모멘텀
- padding: CNN의 패딩
- kernel_size':1: CNN의 커널 크기
- dropout: LSTM에서 탈락
- filters: 초기 필터 수
우리는 200명 이상을 훈련시킬 것 epochs입니다.
5. 하이퍼파라미터 최적화
GAN이 200 epochs에서 학습한 후 MAE(LSTM의 오류 함수인G) 동일한 하이퍼파라미터 세트로 계속 훈련의 하이퍼파라미터를 변경할지 여부를 결정하는 강화 학습에 보상 값으로 전달합니다. 나중에 설명하는 것처럼 이 접근 방식은 RL을 실험하기 위한 것입니다.
RL이 하이퍼파라미터를 업데이트하기로 결정하면 다음으로 가장 기대되는 하이퍼파라미터 세트를 제공하는 베이지안 최적화(아래에서 설명) 라이브러리를 호출합니다.
5.1. 하이퍼파라미터 최적화를 위한 강화 학습
하이퍼파라미터 최적화에서 강화 학습을 사용하는 이유는 무엇입니까? 주식 시장은 항상 변합니다. GAN과 LSTM을 훈련하여 매우 정확한 결과를 생성하더라도 결과는 특정 기간 동안만 유효할 수 있습니다. 즉, 전체 프로세스를 지속적으로 최적화해야 합니다. 프로세스를 최적화하기 위해 다음을 수행할 수 있습니다.
- 기능 추가 또는 제거(예: 상관 관계가 있을 수 있는 새 주식 또는 통화 추가)
- 딥 러닝 모델을 개선합니다. 모델을 개선하는 가장 중요한 방법 중 하나는 하이퍼 매개변수를 사용하는 것입니다(섹션 5 참조). 특정 하이퍼파라미터 세트를 찾은 후에는 이를 변경할 시기와 이미 알려진 세트를 사용할 시기를 결정해야 합니다(탐색 대 착취). 또한 주식 시장은 수백만 개의 매개 변수에 의존하는 연속적인 공간을 나타냅니다.
참고 : 이 노트북의 전체 강화 학습 부분의 목적은 보다 연구 지향적입니다. GAN을 환경으로 사용하는 다양한 RL 접근 방식을 살펴보겠습니다. RL을 사용하지 않고 딥 러닝 모델에서 하이퍼파라미터 최적화를 성공적으로 수행할 수 있는 방법은 많습니다. 하지만... 왜 안돼.
참고 : 다음 여러 섹션에서는 RL, 특히 정책 방법 및 Q-러닝에 대한 지식이 있다고 가정합니다.
5.1.1. 강화 학습 이론
RL의 기본 사항을 설명하지 않고 여기에서 구현하는 특정 접근 방식의 세부 사항으로 건너뛸 것입니다. 우리는 전체 환경을 알지 못하므로 환경이 어떻게 작동하는지에 대한 정의된 모델이 없기 때문에 모델 없는 RL 알고리즘을 사용할 것입니다. 모델을 따르십시오. 우리는 모델 없는 RL의 두 하위 부문인 정책 최적화와 Q-러닝을 사용할 것입니다.
- Q-러닝 - Q-러닝 에서는 주어진 상태에서 조치를 취하는 것의 가치 를 배웁니다 . Q-값 은 조치를 취한 후 예상되는 수익입니다. 7개의 Q 학습 알고리즘을 조합한 Rainbow 를 사용 합니다.
- 정책 최적화 - 정책 최적화에서는 주어진 상태에서 취할 조치를 학습합니다. (배우/비평가와 같은 방법을 사용하는 경우) 주어진 상태에 있는 것의 가치도 배웁니다. 우리는 Proximal Policy Optimization 을 사용할 것 입니다.
RL 알고리즘 구축의 중요한 측면 중 하나는 보상을 정확하게 설정하는 것입니다. 환경의 모든 측면과 환경과 에이전트의 상호 작용을 캡처해야 합니다. 보상 R 을 다음과 같이 정의합니다.
아르 자형이자형승ㅏ아르 자형디=2∗엘영형에스에스G+엘영형에스에스디+ㅏ씨씨유아르 자형ㅏ씨와이G,
어디엘영형에스에스G,ㅏ씨씨유아르 자형ㅏ씨와이G, 그리고엘영형에스에스디Generator의 손실과 정확도, Discriminator의 손실이 각각 입니다. 환경은 GAN과 LSTM 교육의 결과입니다. 다른 에이전트가 취할 수 있는 작업은 GAN의 하이퍼파라미터를 변경하는 방법입니다.디그리고G그물.
5.1.1.1. 무지개
레인보우란?
Rainbow( 링크 )는 7개의 알고리즘을 함께 결합한 Q 학습 기반 오프 정책 심층 강화 학습 알고리즘입니다.
- DQN . DQN은 신경망을 사용하여 Q 값을 나타내는 Q 학습 알고리즘의 확장입니다. 감독(심층) 학습과 유사하게 DQN에서는 신경망을 훈련하고 손실 함수를 최소화하려고 합니다. 전환(상태, 행동, 보상)을 무작위로 샘플링하여 네트워크를 훈련합니다. 레이어는 완전히 연결된 레이어일 뿐만 아니라 예를 들어 컨볼루션 레이어일 수도 있습니다.
- 더블큐 학습 . Double QL은 Q 학습의 큰 문제, 즉 과대 평가 편향을 처리합니다.
- 우선 재생 . 바닐라 DQN에서 모든 전환은 재생 버퍼에 저장되며 이 버퍼를 균일하게 샘플링합니다. 그러나 모든 전환이 학습 단계에서 똑같이 유익한 것은 아닙니다(이는 더 많은 에피소드가 필요하므로 학습을 비효율적으로 만듭니다). 우선 순위가 지정된 경험 재생은 균일하게 샘플링되지 않고 이전 반복에서 더 높은 Q 손실이 있었던 샘플에 더 높은 확률을 제공하는 분포를 사용합니다.
- 결투 네트워크. 결투 네트워크는 두 개의 개별 스트림(즉, 두 개의 서로 다른 미니 신경망을 가짐)을 사용하여 Q 학습 아키텍처를 약간 변경합니다. 하나의 스트림은 가치를 위한 것이고 다른 하나는 장점 을 위한 것 입니다. 둘 다 컨벌루션 인코더를 공유합니다. 까다로운 부분은 스트림 병합입니다. 특수 집계기를 사용합니다( Wang et al. 2016 ).
- 이점 , 공식은ㅏ(에스,ㅏ)=큐(에스,ㅏ)-V(에스), 일반적으로 말하면 행동이 특정 상태에 대한 평균 행동과 비교하여 얼마나 좋은지를 비교하는 것입니다. 어드밴티지는 때로 '잘못된' 행동이 부정적인 보상으로 불이익을 받을 수 없을 때 사용됩니다. 따라서 Advantage 는 평균적인 행동에서 좋은 행동에 대해 더 많은 보상을 시도할 것입니다.
- 다단계 학습. 다단계 학습의 가장 큰 차이점은 N단계 반환(다음 단계의 반환뿐만 아니라)을 사용하여 Q-값을 계산한다는 것입니다. 당연히 더 정확해야 합니다.
- 분포 RL . Q 학습은 평균 추정 Q 값을 목표 값으로 사용합니다. 그러나 많은 경우에 다른 상황에서 Q-값이 동일하지 않을 수 있습니다. Distributional RL은 Q-값의 분포를 평균화하지 않고 직접 학습(또는 근사화)할 수 있습니다. 다시 말하지만, 수학은 그것보다 훨씬 더 복잡하지만 우리에게 이점은 Q-값의 더 정확한 샘플링입니다.
- 시끄러운 그물 . 기본 DQN은 탐색을 수행하기 위해 간단한 𝜀-greedy 메커니즘을 구현합니다. 탐색에 대한 이러한 접근 방식은 때때로 비효율적입니다. Noisy Nets가 이 문제에 접근하는 방식은 노이즈 선형 레이어를 추가하는 것입니다. 시간이 지남에 따라 네트워크는 노이즈를 무시하는 방법을 학습합니다(노이즈 스트림으로 추가됨). 그러나이 학습은 공간의 다른 부분에서 다른 속도로 이루어 지므로 상태 탐색이 가능합니다.
5.1.1.2. PPO
PPO ( Proximal Policy Optimization )는 정책 최적화 모델이 없는 유형의 강화 학습입니다. 다른 알고리즘을 구현하는 것이 훨씬 간단하고 매우 좋은 결과를 제공합니다.
PPO를 사용하는 이유는 무엇입니까? PPO의 장점 중 하나는 값을 통해 간접적으로가 아니라 정책을 직접 학습한다는 것입니다(Q Learning이 Q-값을 사용하여 정책을 학습하는 방식). 그것은 우리의 사용 사례에 적합하고 분포 확률(softmax가 출력으로 추가된 경우)을 학습할 수 있는(평균 및 표준 편차를 통해) 연속 작업 공간에서 잘 작동할 수 있습니다.
정책 기울기 방법의 문제는 단계 크기 선택에 매우 민감하다는 것입니다. 크기가 작으면 진행이 너무 오래 걸립니다(주로 2차 도함수 행렬이 필요하기 때문일 것입니다). 크기가 크면 노이즈가 많아 성능이 크게 저하됩니다. 입력 데이터는 정책의 변경으로 인해 비정적입니다(보상 및 관찰의 분포도 변경됨). 지도 학습과 비교할 때 잘못 선택한 단계는 다음 방문의 전체 분포에 영향을 미치기 때문에 훨씬 더 파괴적일 수 있습니다. PPO는 이러한 문제를 해결할 수 있습니다. 또한 PPO는 다른 접근 방식과 비교하여 다음과 같은 이점이 있습니다.
- 예를 들어 오프 정책 상관 관계 및 재생 버퍼를 유지하기 위한 추가 코드가 필요한 ACER 또는 대리 목적 함수(이전 함수와 새 함수 사이의 KL 다이버전스)에 제약이 있는 TRPO 에 비해 훨씬 덜 복잡 합니다. 정책). 이 제약 조건은 불안정성을 유발할 수 있는 너무 많이 변경하는 정책을 제어하는 데 사용됩니다. PPO는 잘린([1- 𝜖, 1+𝜖] 사이) 대리 목적 함수 를 활용 하고 너무 큰 업데이트에 대한 페널티로 목적 함수를 수정하여 계산(제약에 의해 생성됨)을 줄 입니다.
- TRPO와 비교하여 값과 정책 기능 또는 보조 손실 사이의 매개변수를 공유하는 알고리즘과의 호환성을 제공합니다(PPO에도 신뢰 영역 PO의 이득이 있음).
참고 : 연습의 목적을 위해 PPO 및 기타 포함된 RL 접근 방식의 연구 및 최적화에 너무 많이 들어가지 않을 것입니다. 그보다는 GAN, LSTM 및 CNN 모델에 대한 하이퍼파라미터 최적화 프로세스에 사용 가능한 것을 취하고 맞추려고 노력할 것입니다. 우리가 재사용하고 사용자 정의할 코드는 OpenAI에서 생성되며 여기에서 사용할 수 있습니다 .
5.1.2. 강화 학습에 대한 추가 작업
강화 학습을 더 탐구하기 위한 몇 가지 아이디어:
- 다음에 소개할 첫 번째 항목 중 하나는 대체 알고리즘으로 Augmented Random Search ( link )를 사용하는 것입니다. 알고리즘 작성자(UC, Berkeley 외부)는 PPO와 같은 다른 최신 접근 방식과 유사한 보상 결과를 달성했지만 평균적으로 15배 더 빠릅니다.
- 보상 기능을 선택하는 것은 매우 중요합니다. 위에서 현재 사용하고 있는 보상 기능을 말씀드렸지만 대안으로 다른 기능으로 플레이 해보도록 하겠습니다.
- Berkeley의 AI 연구 팀(BAIR)이 제안한 다중 에이전트 아키텍처를 만듭니다 .
5.2. 베이지안 최적화
최적의 하이퍼파라미터 조합을 찾기 위해 많은 시간이 소요될 수 있는 그리드 검색 대신 베이지안 최적화 를 사용합니다 . 우리가 사용할 라이브러리는 이미 구현되어 있습니다
코드의 다음 부분은 초기화만 보여줍니다.
# Initialize the optimizer
from bayes_opt import BayesianOptimization
from bayes_opt import UtilityFunction
utility = UtilityFunction(kind="ucb", kappa=2.5, xi=0.0)5.2.1. 가우시안 프로세스

6. 결과
from utils import plot_prediction마지막으로 보이지 않는(테스트) 데이터가 프로세스의 여러 단계 후에 입력으로 사용될 때 LSTM의 출력을 비교할 것입니다.
- 첫 번째 에포크 이후에 플로팅합니다.
plot_prediction('Predicted and Real price - after first epoch.')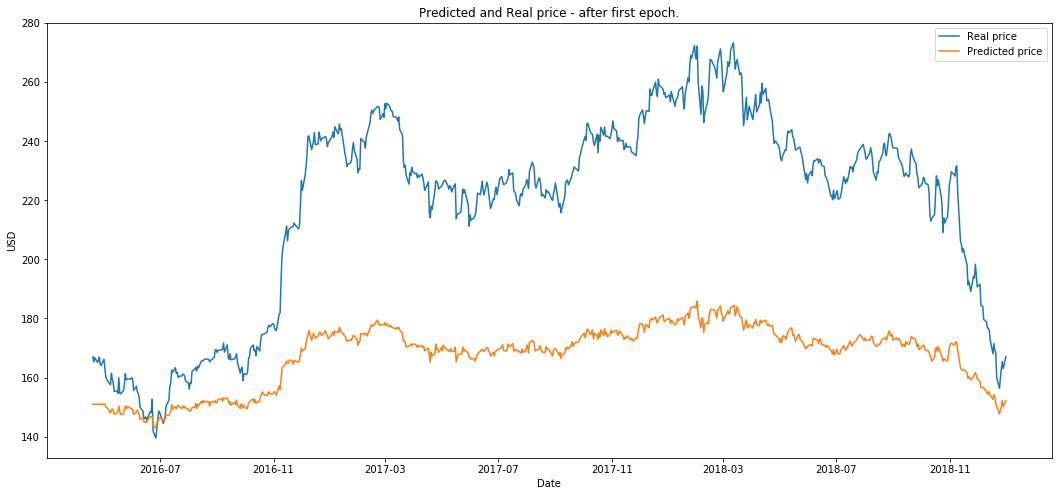
- 50 에포크 이후에 플로팅합니다.
plot_prediction('Predicted and Real price - after first 50 epochs.')
plot_prediction('Predicted and Real price - after first 200 epochs.')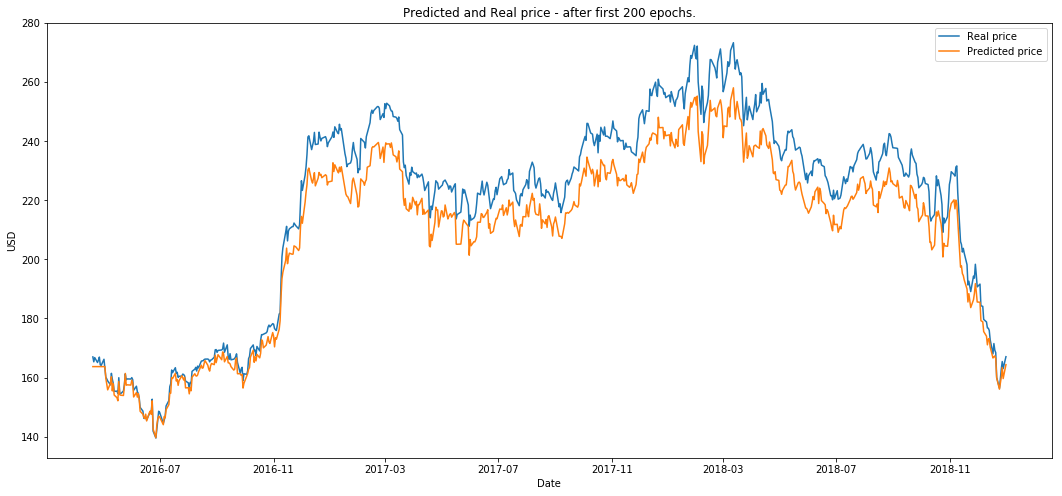
RL은 10개의 에피소드에 대해 실행됩니다(우리는 eposide를 200개의 epoch에 대한 하나의 전체 GAN 교육으로 정의합니다.)
plot_prediction('Final result.')
부인 성명
이 노트는 전적으로 유익합니다. 이 노트북에 제시된 내용 중 어느 것도 특정 증권, 증권 포트폴리오, 거래 또는 투자 전략이 특정인에게 적합하다는 권장 사항을 구성하지 않습니다. 선물, 주식 및 옵션 거래는 상당한 손실 위험을 수반하며 모든 투자자에게 적합하지 않습니다. 선물, 주식 및 옵션의 가치는 변동될 수 있으며 그 결과 고객은 원래 투자한 것보다 더 많은 손실을 입을 수 있습니다.
모든 거래 전략은 귀하의 책임 하에 사용됩니다.
자료출처 : https://github.com/borisbanushev/stockpredictionai
'IT와 과학 > 예측' 카테고리의 다른 글
| 국가 통계량(나라지표)중 인기지표 목록 (0) | 2022.12.04 |
|---|---|
| 열연강판 vs 냉연강판: 차이·용도·선택 가이드 (2025 최신) (0) | 2022.12.04 |
| 2023 트렌트 코리아 핵심 내용 (0) | 2022.11.05 |
| 2022년 13대 주력산업 전망 (0) | 2022.01.15 |
| 2023년 철강가격동향(30년 철강가격 그래프) (1) | 2022.01.15 |



